Combien de rues portent x fois le même nom ? « Un bon croquis vaut qu’un long discours« … cet article aborde le procédé de création d’une visualisation Matplotlib, support d’une analyse sur les ‘occurrences des rues de France.

Et voici le « croquis » 🙂 réalisé avec Matplotlib, à partir des données créées dans la préparation de données. Le graphique représente la répartition par tranches d’occurrences de 268 902 noms de rues pour 786 445 rues. On peut déjà en déduire que l’occurrence moyenne d’une rue française est de 2,92.

Répartition des noms de rues par tranches d’occurrences

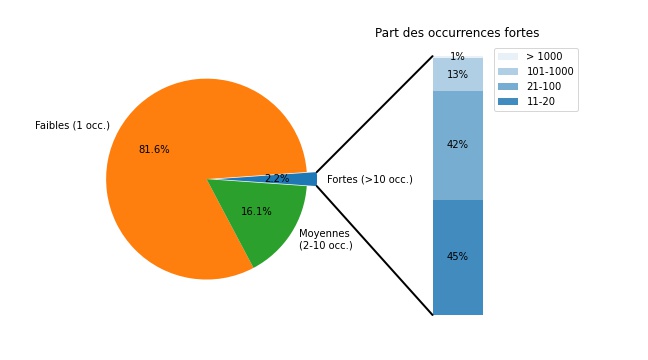
On distingue les occurrences faibles (seulement 1 occurrence) ; les occurrences moyennes (entre 2 et 10 occurrences) et les occurrences fortes (plus de 10 occurrences). On zoom enfin sur ces occurrences fortes.

Comment obtenir ce graphique ? Par du code. Le voici ci-dessous.

Le code

La première étape est de récupérer la donnée préalablement créée : la liste 786 445 rues de France. Puis de créer un dataframe/fichier csv avec le nombre d’occurrences pour chaque nom de rue. Le dataframe dispose de 208 902 entrées.

"""
Objectif : lister le nom de rues avec leur nombre d'occurrences
Outpout : création d'un dataframe et d'un fichier avec le nombre d'occurrence par rues
"""

df = pd.read_csv('/content/fichiertotal.csv')
df = df['RUES'].value_counts().rename_axis('rues').reset_index(name='nombre')
returnValue = df.to_csv('fichiertotal_occurrences.csv', index = False)

On déroule en créant une liste avec, par ordre croissant, le nombre d’occurrences pour i nombres de rues. La liste créée s’appelle ici liste_count. Ainsi liste_count[0] renvoie le nombre de rues à 1 occurrence, liste[1] le nombre de rues à 2 occurrences etc.

"""
Objectif : lister les occurrences dans une liste.
Outpout : création d'une liste qui comporte les nombres d'occurrences de rues par ordre croissant. liste_count[0] donne le nombre de rues à 1 occurrence etc.
"""

df2 = pd.read_csv('/content/fichiertotal_occurrences.csv')
i = 1
max = df2["nombre"].max()
liste_count = []
while i <= max:
    count = df2[(df2['nombre'] >= i) & (df2['nombre'] < (i+1))]['rues'].count()
    liste_count.append(count)
    i = i+1

Pour plus de la clarté r, on détermine des tranches. Et pour chaque tranche correspond une valeur : le nombre de rues compris dans chaque tranche.

"""
Objectif : déterminer les parts d'occurrences par tranches
Outpout : création de tranches d'occurrences par listes
"""

#Tranche-principale de 1 occurrence
tr1 = liste_count[0]

#Tranche-principale de 2 à 10 occurrences
i = 1
while i <= 9:
    if i == 1:
      tr2_10 = liste_count[i]
    else:
      tr2_10 = tr2_10 + liste_count[i] 
    i = i+1

#Tranche-principale de plus de 11 occurrences
tr11p_init = len(df2) - tr1 - tr2_10
tr1 = tr1/len(df2)
tr2_10 = tr2_10/len(df2)
tr11p = tr11p_init/len(df2)

#Sous-tranche 11 à 20 occurrences
i = 10
while i <= 19:
    if i == 10:
      tr11_20 = liste_count[i]
    else:
      tr11_20 = tr11_20 + liste_count[i] 
    i = i+1

#Sous-tranche 21 à 100 occurrences
i = 20
while i <= 99:
    if i == 20:
      tr21_100 = liste_count[i]
    else:
      tr21_100 = tr21_100 + liste_count[i] 
    i = i+1

#Sous-tranche 101 à 1000 occurrences
i = 100
while i <= 999:
    if i == 100:
      tr101_1000 = liste_count[i]
    else:
      tr101_1000 = tr101_1000 + liste_count[i] 
    i = i+1

#Sous-tranche plus de 1001 occurrences
tr1001p = tr11p_init - tr11_20 - tr21_100 - tr101_1000

tr11_20 = tr11_20/tr11p_init
tr21_100 = tr21_100/tr11p_init
tr101_1000 = tr101_1000/tr11p_init
tr1001p = tr1001p/tr11p_init

Enfin on créé le graphique. L’inspiration vient directement de la documentation Matplotlib. Le code se trouve ici. Attention à bien charger la version 3.4.2 de Matplotib (a minima) ! Sinon une erreur apparaît sur le bar_label.

"""
Objectif : paramétrage d'un "Bar of Pie"
Outpout : création et enregistrement d'un graphique
"""

#paramétrage du graphique
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(9, 5))
fig.subplots_adjust(wspace=0)

overall_ratios = [tr11p, tr1, tr2_10]
labels = ['Fortes (>10 occ.)', 'Faibles (1 occ.)', 'Moyennes\n(2-10 occ.)']
explode = [0.1, 0, 0]

angle = -180 * overall_ratios[0]
wedges, *_ = ax1.pie(overall_ratios, autopct='%1.1f%%', startangle=angle,
                     labels=labels, explode=explode)

age_ratios = [tr11_20, tr21_100, tr101_1000, tr1001p]
age_labels = ['11-20', '21-100', '101-1000', '> 1000']
bottom = 1
width = .2

for j, (height, label) in enumerate(reversed([*zip(age_ratios, age_labels)])):
    bottom -= height
    bc = ax2.bar(0, height, width, bottom=bottom, color='C0', label=label,
                 alpha=0.1 + 0.25 * j)
    ax2.bar_label(bc, labels=[f"{height:.0%}"], label_type='center')

ax2.set_title('Part des occurrences fortes')
ax2.legend()
ax2.axis('off')
ax2.set_xlim(- 2.5 * width, 2.5 * width)

theta1, theta2 = wedges[0].theta1, wedges[0].theta2
center, r = wedges[0].center, wedges[0].r
bar_height = sum(age_ratios)

x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = r * np.sin(np.pi / 180 * theta2) + center[1]
con = ConnectionPatch(xyA=(-width / 2, bar_height), coordsA=ax2.transData,
                      xyB=(x, y), coordsB=ax1.transData)
con.set_color([0, 0, 0])
con.set_linewidth(2)
ax2.add_artist(con)

x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = r * np.sin(np.pi / 180 * theta1) + center[1]
con = ConnectionPatch(xyA=(-width / 2, 0), coordsA=ax2.transData,
                      xyB=(x, y), coordsB=ax1.transData)
con.set_color([0, 0, 0])
ax2.add_artist(con)
con.set_linewidth(2)

#Enregistrement et affichage du graphique
plt.savefig('croquis.jpg')
plt.show()

Ce qui nous donne le graphique ci-dessus. Et un fichier nommé « croquis.jpg »

L’analyse

Que constate-t-on ?

1/ Déjà qu’une majorité de rues (81,6 %) porte un nom unique. Cette proportion tendrait à souligner le caractère essentiellement local de ce type de voirie. Instinctivement, on pourrait imaginer une proportion moindre. Et se dire qu’une analyse des avenues, dont on peut supposer qu’elles portent davantage de noms à résonnance nationale, serait différente. Nous pouvons pourtant voir les choses différemment… mettre notre graphique « en perspective », et considérer que ces 219 994 rues « uniques » ne représentent « que » 27,8 % des 786 445 rues de France. Ce renversement souligne davantage le « poids » que représente les rues à plusieurs occurrences. Et l’analyse du point suivant devient tout d’un coup plus croustillante 🙂

2/ Nous comptabilisons 5 984 rue à occurrences fortes (plus de 10 occurrences) soit seulement 2,2 % des noms de rues. Pis ! Seulement 1 % (43 rues) de ce 2,2 % a « plus de 1 000 occurrences« . C’est pourtant ici, dans ces pourcentages infinitésimaux que se nichent l’essence même des noms qui relient notre imaginaire commun. Et avec quelle force ! Comme pour le point précédent, ces « petits » pourcentages peuvent être vu différemment. Ainsi les 5 984 noms de rues à occurrences fortes représentent… 54,3 % de toutes les rues de France ! Autrement dit plus de la moitié de nos rues représente moins de 3 % de nos noms de rues. Comment déterminer cette proportion ?

Par le code :

"""
Objectif : obtenir le % des occurrences par tranches de rues
Outpout : un %
"""

#Ici pour les rues à occurrences fortes (> 10 occurrences). L'output est 0,54309...
df3 = df2[ df2['nombre'] > 10 ]
sumdf = df['nombre'].sum(axis = 0, skipna = True)
sumdf3 = df3['nombre'].sum(axis = 0, skipna = True)
part_tranche = sumdf3/sumdf
part_tranche

Nous pouvons enrichir notre croquis comme suit :

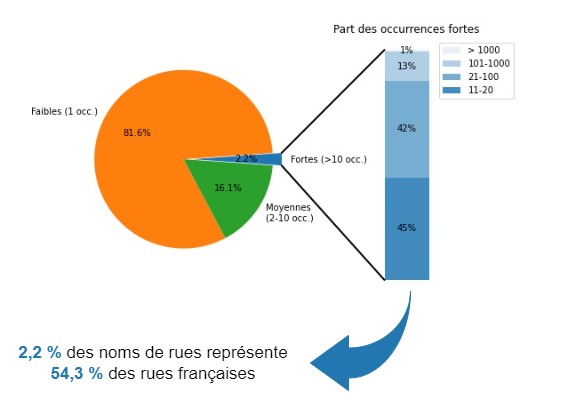
De même, les 0,022 % de rues à plus de 1 000 occurrences, la crème de la crème, représente 10,8 % de toutes nos rues ! Le poids des noms n’est pas celui des occurrences… Mais quelles sont ces rues ? Sont-ce des personnages ? Des symboles ? Des lieux ? Des plantes ? L’analyse ne le dit pas… du moins pas celle-ci. On y verra plus clair dans une autre analyse : celle du Top 100 des rues les plus répandues en France.